The scheme of numbers forming Pascal’s triangle was known long before Pascal’s time. The Persian mathematician Al-Karaji (953-1029) wrote a now lost book containing the first formulation of binomial coefficients and the first ever description of Pascal’s triangle Later the triangle was also studied by Omar Khayyam around 1100, so in Iran this scheme is called Khayyam’s triangle (Persian: مثلث خیام).
Mention of a triangular sequence of binomial coefficients called meru-prastaara is also found in the 10th century Indian mathematician Halayudha’s commentary on the works of another mathematician, Pingala. In 1303 the book “Jasper Mirror of the Four Elements” by the Chinese mathematician Zhu Shijie was published, in which Pascal’s triangle was depicted in one of the illustrations; it is believed that another Chinese mathematician, Yang Hui, invented it, so in China it is called Yang Hui’s triangle.
Properties of Pascal’s triangle
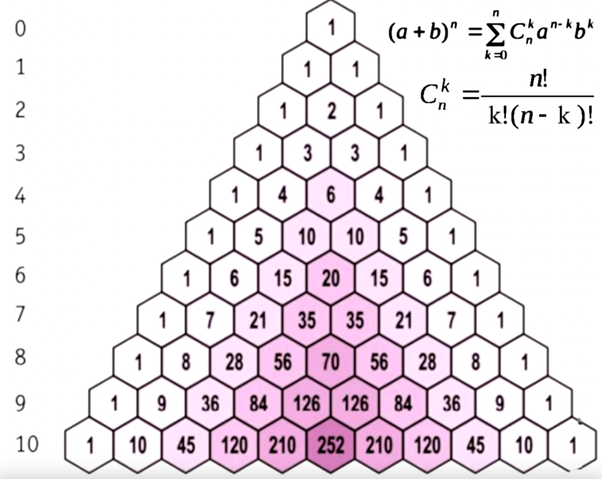
- The sum of the numbers of the -th row (counting from zero) of Pascal’s triangle is equal to . Indeed, when passing from each line to the next, the sum of members doubles, and for the zero line it is equal to .
- All the rows of Pascal’s triangle are symmetric. Because when passing from each line to the next, the property of symmetry is preserved, and the zero line is symmetric.
- Each number in Pascal’s triangle is equal to , where – the number of the line, – the number (counting from zero) of the element in the line.
- Each number of Pascal’s triangle reduced by one is equal to the sum of all numbers filling the parallelogram bounded by the diagonals at the intersection of which this element is located.
- Along the diagonals parallel to the sides of the triangle are lined up triangular numbers, tetrahedral numbers, etc.
- If we calculate for each ascending diagonal of Pascal’s triangle the sum of all numbers standing on this diagonal, we get the corresponding Fibonacci number.
Basic applications of Pascal’s triangle
- Binomial coefficients:
- The numbers in Pascal’s triangle represent the binomial coefficients when decomposing the binary term (a + b)ⁿ
- This is widely used in algebra when working with polynomials
- Probability Theory:
- Helps calculate probabilities in Bernoulli’s scheme (independent trials)
- Used to calculate the binomial distribution
- Used in combinatorial problems
- Combinatorics:
- Allows you to find the number of combinations C(n,k)
- Helps solve problems on counting different combinations and placements
- Used in solving problems about paths on a lattice
- Computer Science:
- Used in dynamic programming algorithms
- Used in coding theory
- Helps in the optimization of some algorithms
- Mathematical Analysis:
- Used in decomposing functions into series
- Used in Newton’s binomial formula
- Helps in numerical methods
Interesting fact: Pascal’s triangle also finds application in:
- Music theory (rhythmic structures)
- Architecture (proportions and symmetry)
- Computer graphics (Bézier curves)
- The Plinko slot machine is based on Pascal’s triangle
Conclusion
Thus, Pascal’s triangle is a unique mathematical structure with many remarkable properties and a wide range of practical applications. Its versatility is manifested both in pure mathematics (combinatorics, algebra) and in applied areas (probability theory, computer science).
Of particular value is the relationship of Pascal’s triangle to other mathematical sequences such as the Fibonacci numbers, triangular and tetrahedral numbers. This mathematical construct continues to find new applications in modern fields of science and technology, from computer graphics to music theory, demonstrating its continuing importance in the development of mathematical science.
FAQ
Question: How are Fibonacci numbers and Pascal’s triangle related?
Answer: If you count the sum of numbers along the ascending diagonals of Pascal’s triangle, you will get the corresponding Fibonacci number.
Question: What is the basic property of symmetry inherent in Pascal’s triangle?
Answer: All rows of Pascal’s triangle are symmetric about the central vertical, and this property is preserved when moving from each row to the next.
Question: How is any element of Pascal’s triangle calculated?
Answer: Each number in Pascal’s triangle is equal to C(n,k), where n is the number of the line, k is the number of the element in the line (counting from zero).
Question: What is the sum of the numbers in the nth row of Pascal’s triangle? Answer: The sum of the numbers in the nth row is 2ⁿ, because the sum of the terms doubles as you move from each row to the next.



Be First to Comment